La Stabilità dei Sistemi di Controllo

L'analisi e la sintesi dei sistemi di controllo considerati in questi appunti farà sempre riferimento a sistemi lineari, stazionari , di ordine finito . Considerando quindi la rappresentazione in spazio di stato nel caso di sistemi a tempo continuo, questa sarà del tipo differenziale: 

Le definizioni di stabilità si riferiranno a questa rappresentazione, ma in seguito si passerà alla rappresentazione esterna mediante funzioni di trasferimento : il criterio di Nyquist verrà formulato a partire dalla funzione di trasferimento in catena diretta F(s). Il passaggio da una rappresentazione all'altra si ottiene scrivendo le espressioni dell'evoluzione dello stato e dell'uscita :

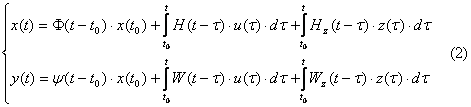ed effettuandone la trasformazione secondo Laplace :

La stabilità interna riguarda la limitatezza della risposta x(t) descritta in (2) rispetto a perturbazioni dello stato iniziale. In generale la stabilità interna è una proprietà che riguarda una traiettoria e dipende quindi dallo stato iniziale e dall'ingresso. Fra tutte le traiettorie, quelle più interessanti da studiare sono i punti di equilibrio ( un punto si dice di equilibrio se , per almeno un ingresso, la traiettoria che ha origine nel punto coincide col punto stesso ), perché lo studio della stabilità di una qualsiasi traiettoria si può ricondurre allo studio della stabilità di un punto di equilibrio( considerando il sistema errore ).
Un punto di equilibrio xe si dice stabile se , comunque prendiamo  , esiste  tale che , se  , allora  in ogni istante di tempo successivo all'istante iniziale. In particolare, considerando sistemi tempo-invarianti , si può prendere l'istante iniziale nullo. Se, oltre ad essere verificata la condizione precedente, esiste anche  tale che  , allora il punto di equilibrio si dice asintoticamente stabile. 
Nei sistemi lineari la stabilità di un qualsiasi movimento equivale alla stabilità dell'origine del sistema libero associato ( B,M=0 in (1) ) , pertanto si può parlare di stabillità del sistema (che nel caso generale è invece una dicitura impropria) . In base alla definizione precedente, quindi , il sistema è stabile se comunque prendiamo  , esiste  tale che , se  , allora  in ogni istante di tempo successivo a quello iniziale .

La stabilità esterna o BIBO ( bounded input, bounded output ) si ha se , comunque prendiamo un limite superiore per l'ingresso  e uno stato iniziale  , allora esiste un limite superiore per l'uscita  , cioè se è  allora .
Si intuisce facilmente che questa condizione può essere verificata anche se una componente dello stato è illimitata ma , per questioni di osservabilità , non produce effetti sull'uscita , pertanto la stabilità esterna è una condizione meno stringente della stabilità interna : se un sistema lineare è stabile internamente nell'origine allora è anche esternamente stabile . Perché valga il viceversa deve invece essere verificata anche l'osservabilità , perciò un sistema stabile esternamente e osservabile è anche stabile internamente.

La stabilità BIBO nell'origine è una proprietà ancora meno stringente della stabilità BIBO : nella definizione precedente, infatti, l'illimitatezza della y(t) poteva dipendere tanto dall'ingresso quanto dallo stato iniziale  . Se la condizione iniziale viene presa nulla si perviene alla seguente definizione : un sistema lineare si dice stabile esternamente nell'origine se , comunque si prende  esiste un  tale che , se l'ingresso è limitato superiormente da M ( ) , allora anche l'uscita è limitata superiormente da Nm ( ) . 
Se un sistema è stabile esternamente è anche stabile esternamente nell'origine, mentre perché valga il viceversa deve essere soddisfatta la condizione di raggiungibilità : se un sistema è stabile esternamente nell'origine e raggiungibile , allora è anche stabile esternamente.

Nel proseguio di questi appunti si studierà la stabilità dei sistemi di controllo a partire dalla rappresentazione esterna ingresso/uscita , cioè mediante la funzione di trasferimento W(s) in (2). L'unica stabilità che si può dedurre da questa funzione è la stabilità esterna con condizione iniziale nulla : d'ora in poi s'ipotizzerà pertanto che i sistemi studiati siano raggiungibil ed osservabili . Per quanto detto finora, si può infatti affermare che se un sistema è raggiungibile ed osservabile allora la stabilità esterna con condizione iniziale nulla equivale alla stabilità interna, come mostrato in figura 1.

I requisiti di un sistema di controllo : fedeltà di risposta e stabilità

Quando si affronta la sintesi di un sistema di controllo i due requisiti fondamentali che vanno soddisfatti sono :

- la stabilità . A breve saranno date le definizione rigorose di stabilità : intuitivamente si può vedere la stabilità come la capacità del sistema di reagire a perturbazioni limitate con risposte limitate . Le perturbazioni possono essere variazioni delle condizioni iniziali o degli ingressi , mentre la risposta può essere nello stato o in uscita : si parla così di stabilità interna nell'origine, di stabilità esterna , di stabilità esterna nell'origine .

- la fedeltà di risposta , cioè la capacità del sistema di produrre uscite conformi a quelle desiderate . Tale conformità va studiata in relazione agli ingressi forniti al sistema, ai disturbi e alle variazioni parametriche.

Si intuisce come , prima di affrontare la sintesi del controllore , un corso di Controlli Automatici debba fornire gli strumenti per quantificare questi due requisiti , mediante un'opportuna analisi dei sistemi di controllo: si perverrà quindi a concetti come il margine di fase e margine di guadagno ( per quantificare la stabilità ) o ai parametri per descrivere la risposta in regime transitorio e in regime permanente, o ancora alla sensibilità che quantifica la reazione del sistema alle variazioni parametriche.

L'analisi che seguirà nei prossimi paragrafi sarà comunque costantemente "orientata alla sintesi" :

- lo studio della stabilità terrà conto del fatto che lo schema di controllo più diffuso è quello a controreazione e ci si chiederà quali condizioni deve rispettare la funzione di trasferimento in catena aperta F(s) perché il sistema a ciclo chiuso sia stabile ( criterio di Nyquist ).

- non potendo caratterizzare in modo esaustivo la risposta del sistema ( è impensabile considerare l'andamento analitico della risposta per tutti i possibili ingressi o disturbi ) , ci si limiterà a considerare le classi di stimoli più diffuse nei sistemi di controllo : il gradino unitario per la risposta transitoria, i polinomi e le sinusoidi per la risposta a regime permanente (tali restrizioni non sono comunque eccessivamente limitanti finché si resta nell'ambito dei sistemi lineari stazionari. Diversa è la questione passando a considerare sistemi non lineari) . Allo stesso tempo la caratterizzazione della risposta del sistema avverrà mediante pochi parametri significativi ( tempo di salita , sovraelongazione , tempo di assestamento ) che avranno un immediato corrispettivo in alcune caratteristiche del controllore da progettare ( banda passante , modulo alla risonanza della funzione di trasferimento in catena aperta).

Esempi di schemi di controllo e proprietà del controllo in controreazione

 

Per chiarire il significato degli schemi di controllo presentati nel paragrafo precedente , ed evidenziarne pregi e difetti, si può considerare come esempio il controllo del livello del liquido in un serbatoio. Il serbatoio eroga un flusso nominale Qu verso una rete utilizzatrice : la variabile controllata è il livello L , mentre la variabile controllante è il flusso in entrata Qi ( Qu è un parametro del modello , sul quale non è consentito agire ). Le tre strategie si traducono nelle seguenti azioni di controllo:

- il controllo in catena aperta consiste nel fornire al serbatoio un flusso in entrata pari al flusso nominale in uscita. Se però la rete utilizzatrice presentasse per un certo intervallo di tempo un fabbisogno inferiore a quello nominale , i due flussi non si compenserebbero ed il livello del serbatoio tenderebbe a salire oltre il valore desiderato ( col rischio di un overflow ). Questa situazione è mostrata in figura 1.

- il controllo con compensazione diretta consiste nel misurare con un rivelatore di portata il flusso in uscita Qu e fornire in ingresso lo stesso valore per Qi . Questa soluzione ovvia al problema delle variazioni dovute al fabbisogno della rete utilzzatrice, ma non è in grado di rilevare, ad esempio, possibili variazioni dovute all'evaporazione del liquido o ad eventuali perdite nel serbatoio. Questa situazione è mostrata in figura 2. 

- l'unica soluzione che permette di rilevare tutti questi disturbi agenti sul sistema è l'introduzione di un galleggiante , o di un qualsiasi altro trasduttore di livello, in modo da calcolare il flusso in entrata come funzione della differenza L-Ldes ( segnale errore ). Questa scelta corrisponde allo schema di controllo in controreazione ( figura 3 )

L'esempio evidenzia due delle proprietà fondamentali del controllo a controreazione:

- riduzione degli effetti dovuti a variazioni parametriche nel modello del processo ( ad esempio le variazioni del flusso in uscita ) ; 

- riduzione dell'effetto dei disturbi in uscita al processo ( ad esempio le variazioni dovute all'evaporazione e alle perdite del serbatoio ) . 

Il caso del serbatoio permette inoltre di esemplificare uno dei limiti entrinseci della controreazione stessa : la necessità di una informazione attendibile sull'uscita. Si dimostrerà in seguito che l'errore di trasduzione si può schematizzare come un rumore additivo sul ramo di retroazione : a differenza dei disturbi in uscita e nel ramo diretto, che possono essere ridotti dalla retroazione progettando opportunamente il controllore, questo genere di disturbi si ripercuote interamente sull'uscita . Tornando all'esempio del serbatoio, perché il sistema di controllo mantenga con buona approssimazione il livello del liquido attorno al valore desiderato è necessario scegliere un buon galleggiante o un buon trasduttore di livello.

 

Introduzione all'automatica

 

In automatica controllare un sistema significa calcolare un’azione o una sequenza di azioni che facciano assumere ad una grandezza di interesse un opportuno valore o una opportuna sequenza di valori. Tale grandezza viene detta grandezza controllata e riguarda solitamente un processo fisico , il processo da controllare. Nel corso di Controlli Automatici si guarda al processo secondo l’approccio della teoria dei sistemi; lo si considera cioè un oggetto astratto orientato dotato di ingressi ed uscite : le uscite sono le grandezze da controllare e gli ingressi sono le grandezze controllanti . In questo modo è possibile stimare un modello del processo a partire dal quale si calcola l’azione di controllo .

Si parla di controlli automatici perché il calcolo e l’attuazione dell’azione di controllo vengono svolti da dispositivi che sostituiscono del tutto o in parte l’azione dell’uomo. L’insieme di questi dispositivi viene solitamente indicato col nome di controllore, che nei controllori più semplici ha la struttura indicata in figura 2.

Tale schema , che viene detto controllo in catena aperta , da luogo a prestazioni scadenti e trova impiego solo in situazioni particolari ( ad esempio quando l’attuatore è un motore passo-passo) , perché non tiene conto dello scostamento fra uscita reale e uscita del modello. Questo scostamento è dovuto sostanzialmente a due cause : 

- il modello del processo non può essere conosciuto con esattezza ( dinamica non modellata e variazioni parametriche nel modello del processo ) ;

- sul sistema agiscono rumori e disturbi che non sono completamente noti . 

 

Per questo motivo nei controlli automatici si preferisce adottare lo schema a controreazione , mostrato in figura 3, che calcola l’azione di controllo a partire dalla differenza fra uscita desiderata e uscita effettiva . Questa differenza viene detta segnale errore : il compito del controllore è proprio quello di far tendere a zero il segnale errore , soddisfando alcune specifiche sulle prestazioni globali del sistema , che saranno descritte più avanti. Se anziché la differenza si effettuasse la somma fra ingresso e uscita del sistema si parlerebbe di reazione positiva e non di reazione negativa o controreazione. La reazione positiva trova scarsa applicazione in controlli automatici , perché causa di instabilità : in elettronica questa instabilità viene invece sfruttata per realizzare gli oscillatori.

E' possibile anche una terza strategia di controllo, che si applica quando è verificata una condizione particolare : si hanno informazioni a priori sui disturbi che agiscono sul processo. Il disturbo deve quindi essere parzialmente noto o almeno misurabile e allora si parla di schema di controllo a compensazione diretta , che è mostrato in figura 4.

I sistemi basati esclusivamente sulla compensazione diretta sono comunque relativamente rari , perché presentano svantaggi simili al controllo in catena aperta : se l'informazione sul disturbo si degradasse o se l'azione di controllo fosse diversa da quella progettata, non si avrebbe alcun riscontro sul reale andamento dell'uscita. Per questo motivo , quando si conosce almeno in parte il disturbo agente sul processo, si preferisce combinare i vantaggi del controllo a compensazione diretta con quelli del controllo in catena chiusa ricorrendo ad uno schema di controllo ibrido come quello mostrato in figura 5.